В основе всех архитектур глубокого обучения лежит многослойный перцептрон (MLP). У него есть веса и нейроны, в которых расположены функции активации. Этой парадигмой ученые пользуются с 1957 года, когда ее предложил Фрэнк Розенблатт. 

Сейчас, спустя 67 лет, исследователи из MIT представили альтернативу MLP – новую архитектуру нейронной сети, получившую название Kolmogorov-Arnold Networks (KAN), в которой реализовано перемещение активаций на «ребра» сети. 

С момента выхода статьи не успело пройти и суток, но она уже превратилась в сенсацию. И неудивительно, ведь изменения в парадигме перцептрона влекут за собой изменения во всем глубоком обучении, и могут перевернуть в том числе большие языковые модели и системы компьютерного зрения.

Однако, если вам захочется детальнее разобраться с тем, как работает новинка, и вы заглянете в статью, то увидите там почти 50 страниц текста, включающих много сложных формул и обозначений.

В общем, эта статья поможет разобраться с устройством KAN и не сойти с ума. Поехали!

Как работает перцептрон

Для начала давайте вспомним базовую вещь: нейросети работают с функциями. В любой задаче обучения с учителем у нейросети есть обучающая выборка, состоящая из пар {x_i, y_i}, где x - это входные данные, а y - "ответ". Задача сети - найти такую многомерную функцию f, что f(x_i) ≈ y_i для всех точек пространства. Другими словами, нейросеть пытается найти функцию, обобщающую связь между входами и выходами задачи.

Архитектура классического перцептрона предполагает поиск такой функции с помощью линейных слоев, на которых выполняется умножение входов на веса ребер, и функций активации в нейронах.

Такая архитектура основана на теореме Цыбенко (universal approximation theorem), которая доказывает, что нейронная сеть может аппроксимировать любую непрерывную функцию с любой точностью. Однако есть и другие теоремы, связанные с аппроксимацией функций. С одной из них – теоремой Колмогорова-Арнольда, как раз и связан KAN.

Теорема Колмогорова-Арнольда

Чтобы точно понять строение KAN, нужно разобраться с математикой. Но обещаем, эта часть будет нескучной и совсем не сложной.

Итак, заслуга Колмогорова и Арнольда заключается в том, что они доказали, что аппроксимация непрерывной ограниченной функции от множества переменных сводится к нахождению полиномиального числа одномерных функций:

Казалось бы: это отличная новость для машинного обучения: получается, чтобы "воссоздать" большую страшную функцию связи между входами и выходами сети, нам нужны обычные одномерные функции, число которых с ростом параметров к тому же растет полиномиально, а не экспоненциально.

Однако, не все так просто.

• Во-первых, наши одномерные функции могут оказаться негладкими и даже фрактальными, и их будет невозможно обучить.
• Во-вторых, число таких функций и глубина композиции в теореме фиксированы, а значит наша нейронная сеть будет иметь всегда один и тот же размер (2 слоя и 2n+1 нейронов на них). Получается, что подход совсем деревянный и не масштабируется.

Именно эти два пункта раньше останавливали ученых, которые пробовали применять Колмогорова-Арнольда в ML. Да-да, идея не новая, но по-настоящему развили ее только сейчас: в отличие от предшественников, авторы KAN придумали, как обойти проблемы, и в итоге получили блестящий результат. Итак, давайте посмотрим, что они сделали.

Наивная архитектура KAN

Сначала исследователи, как и другие ученые до них, пытались использовать теорему из предыдущего раздела "в лоб". Так как мы должны найти только функции, в этом случае у нас получается нейросеть, у которой вообще нет линейных весов и функций активации в нейронах. Здесь все наоборот. Вместо весов на ребрах сети мы обучаем функции, а в нейронах просто их складываем.

Вот пример: для сети с двумя (n=2) входными параметрами мы получаем двухслойную (так как глубина композиции в теореме равна двум) нейросеть с пятью (так как в теореме участвует 2*n+1 = 5 функций) нейронами на скрытом слое.

"А что там с тем, что функции могут быть необучаемыми?" - спросите вы. Ну, во-первых, авторы обосновали, что в случае предсказания зависимостей из реального мира появление таких функций крайне маловероятно. Во-вторых, чтобы обойти эту проблему, в KAN мы ищем не абы какие функции, а параметризуем их сплайнами.

Сплайн – это такая гладкая кривая, кусочно-полиномиальная функция, которая на разных отрезках задается различными полиномами. Каждый сплайн аппроксимируется с помощью заданного количества точек. Чем больше точек - тем точнее аппроксимация.

Сплайны непрерывны и дифференцируемы, а значит, такую архитектуру можно спокойно обучать с помощью привычного нам метода обратного распространения ошибки.

Обобщенная архитектура

В отличие от проблемы дифференцируемости, которую ученые элегантно решили сплайнами, проблема с масштабируемостью KAN не сдалась так легко. Как сделать так, чтобы в сеть можно было добавить больше слоев и нейронов? Ведь для этого нужна обобщенная теорема Колмогорова-Арнольда, а ее просто-напросто не существует.

Вот тут и заключена прорывная часть работы. Исследователи заметили, что по аналогии с перцептроном мы можем на каждом слое построить матрицу обучаемых объектов. Просто в нашем случае это будут не параметры (числа), а функции. В терминах матрицы исходная формула оказывается не законом, а просто частным случаем KAN с двумя слоями. А обобщенный KAN – это более глубокая композиция таких матриц:

А саму теорему для KAN можно переписать вот так:

В остальном, кроме изящной внутренней математики, работать с KAN можно также, как с обычными сетями: добавлять и удалять нейроны, стекать слои, использовать дропаут и даже регуляризацию.

Сравнение с перцептроном

Перемещение активаций на ребра хотя и не кажется глобальным изменением, но все-таки несет в себе много перемен. Вот ключевые аспекты, отличающие KAN от перцептрона:

• Так как для аппроксимации каждого сплайна требуется несколько точек (пусть таких точек у нас K штук), KAN требует в K раз больше параметров, чем MLP с той же глубиной и количеством нейронов на слоях.
• К счастью, проблема из первого пункта нивелируется тем, что KANу требуется во много раз меньше нейронов, чтобы достичь точности MLP. Исследователи также опытным путем доказали, что KAN гораздо лучше генерализует данные.
• За счет того, что в KAN мы обучаем функции, а не числа, можно повысить точность сети без переобучения ее с нуля. В MLP, чтобы добиться лучшей точности, мы можем увеличивать количество слоев и нейронов, но это требует полноценного ретрейнинга и вообще-то работает далеко не всегда. В KAN достаточно просто добавить больше точек в сетку аппроксимации. Это гарантирует лучший результат, и при этом не нужно переучивать нейросеть.
• KAN более интерпретируем, чем MLP. А ведь интерпретируемость – это одна из главных проблем современных нейросетей.
• KAN лучше справляется с аппроксимацией сложных математических функций, поэтому у него, можно сказать, "технический склад ума". В статье показано, что KAN на порядок лучше решает дифференциальные уравнения и может (пере)открыть законы физики и математики.
• У архитектуры есть бутылочное горлышко: KAN учится медленнее MLP примерно в 10 раз. Возможно, это станет серьезным камнем преткновения, а возможно инженеры быстро научатся оптимизировать эффективность таких сетей.

Код!

Статья – это еще не все. Исследователи также выложили код, и даже зарелизили библиотеку, с помощью которой можно поиграть с KAN из коробки, она называется pykan. Документацию к ней можно найти здесь.

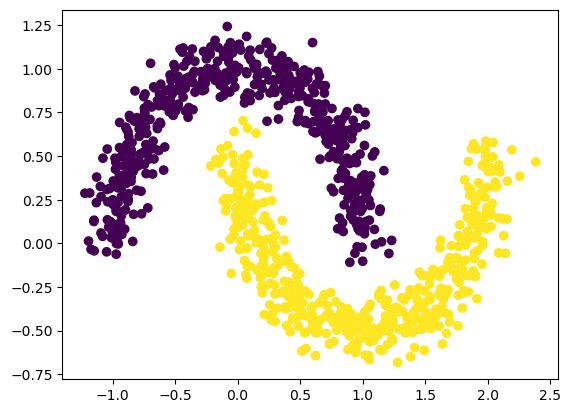
Давайте для примера посмотрим, как обучить KAN для задачи классификации. Сначала сгенерируем датасет:

from kan import KAN
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch
import numpy as np

dataset = {}
train_input, train_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)
test_input, test_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)

dataset['train_input'] = torch.from_numpy(train_input)
dataset['test_input'] = torch.from_numpy(test_input)
dataset['train_label'] = torch.from_numpy(train_label[:,None])
dataset['test_label'] = torch.from_numpy(test_label[:,None])

X = dataset['train_input']
y = dataset['train_label']
plt.scatter(X[:,0], X[:,1], c=y[:,0])

А теперь легким движением руки обучим KAN:

model = KAN(width=[2,1], grid=3, k=3)

def train_acc():
    return torch.mean((torch.round(model(dataset['train_input'])[:,0]) == dataset['train_label'][:,0]).float())

def test_acc():
    return torch.mean((torch.round(model(dataset['test_input'])[:,0]) == dataset['test_label'][:,0]).float())

results = model.train(dataset, opt="LBFGS", steps=20, metrics=(train_acc, test_acc));

Точность на этом примере составит единицу на тренировочной и тестовой выборке.

Кстати, в репозитории проекта лежит очень красивые и понятные ноутбуки, в которых можно найти туториалы по библиотеке и кейсы использования KAN.

Заключение

KAN — это новая эра глубокого обучения? Точного ответа нет, но у метода есть все шансы. Как минимум это большой толчок для исследований. Будем ждать новостей об возможностях для улучшения существующих моделей.